In my previous post on the Deep Learning Summit in Boston, I discussed Maithra Raghu’s phenomenal insight into neural networks and the practical upshot that perspective had for the model training process. Now, let’s delve into a more theoretical discussion surrounding these new insights, and demonstrate that neural networks aren’t the black boxes many seem to suggest they are.
Raghu’s results actually follow from the oft forgotten universal approximation theorem (UAT). I say forgotten because, while it’s popular to cite the UAT, it’s even more popular to state that it’s over-cited and inconsequential, even by the inimitable Chris Olah and Andrej Karpathy. The details of the theorem aren’t important here – I’ll just explain the upshot. Fundamentally, neural networks are built to approximately learn a function. As a physicist in a former life, my bread and butter for approximating functions was breaking out what’s called a “basis expansion,” which simply capitalizes on the fact that a function is algebraically a type of vector, and is thus in the span of other functions. That is, to explain the terms of art: a basis expansion expresses one complicated function as the sum of simpler functions, the ‘basis’ functions. It’s not unlike forming green (the function of interest) by adding blue and yellow (the basis functions).
If we choose the basis functions judiciously, it’s very simple to find the sum that aptly approximates the function we sought to learn (printers are good at making many colors by mixing three simple ones)! But…how do we know which set of functions is best to choose when performing this basis expansion (like choosing which colors to use in a painting palette)?
This is where the universal approximation theorem comes in. One interpretation is that neurons furnish a means of selecting a very general set of appropriate basis functions. However, these functions must be learned – that is, there are unspecified parameters in them be best chosen to match the data. That’s part of the value added by neural networks over traditional basis function techniques: they learn the best basis functions! Raghu’s understanding of the intralayer (explicitly: within a single layer; see Fig. 1) structure of neural networks, motivated by the universal approximation theorem, has an advantage over an interpretation predicated on the existence of a sample of inputs that generates outputs by passing through the neurons: we need no sample set to discuss the vector structure of layers in a network! This circumvents what I worry may become a red herring within the field: procuring data in an unnatural way to manipulate the vector structure of layers. It’s worth stating that discussing neural networks using this language is not common with the literature, but I believe will be in short time.
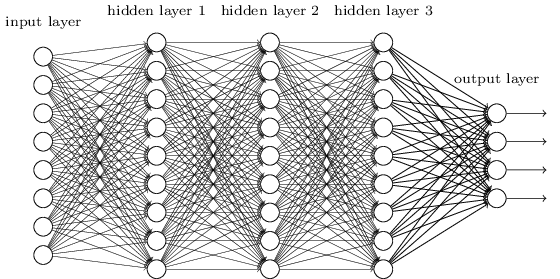
Fig 1. The structure a ‘multi-layer’ neural network. Each circle represents a neuron (a basis function), and each line indicates how the output of that neuron is passed to the right. Notice it’s made of ‘layers’ of neurons.
Now, if vectors comprise the intralayer structure of a neural network, what about the interlayer structure (what goes on between the layers)? Moreover, if a single layer can learn a function, considering the universal approximation theorem, why is there all this clamor over adding more layers to a network? The math involves something called group theory, which is a little harder to bring into layman parlance; however, I like to relay the utility of employing multiple layers using a very layman example: the Rubik’s cube. If I handed you a Rubik’s cube in some initial, highly disordered state and asked you to figure out how to solve it in one go, I’d be asking you to find a very complicated function. It would probably be easier to first figure out how to take that arbitrary state and solve a single side first; then, figure out how to solve another face; then another, and so on until the Rubik’s cube is completed. Solving each face can be thought of as finding a simpler function that reduces the disorder of the cube a little bit at a time instead of trying to find a difficult one that reduces it all at once. This is like adding layers to a network. Each layer successively learns how to solve one face of the cube until it’s finished! This furnishes a nice guiding principle in designing network architectures: the structure of layers in a network can be inspired by how we might, as humans, tackle a problem in small steps.
To this end, we would expect that if the first layer can reduce the disorder a lot, it will. It’s like giving you the tools to solve two faces of the cube at once instead of just one – if you easily can, you probably would, right? This will bring the actual state of the Rubik’s cube a little closer to the desired state. However, this actually makes it harder for the rest of the network to figure out how to make the cube a little more ordered. This is demonstrated in Fig 2., which shows the iterative reduction in the disagreement between the network’s predictions and the correct data predict. Notice that the better the loss (i.e. the less disordered the cube is), the more slowly the disorder is reduced. It’s like starting with a very messy room compared to a mostly clean one – it’s easy to vacuum up a lot of dirt when there’s a lot already on the floor, but it’s harder to figure out how to clean up more when there are just a few hidden dirty spots off in the corner or behind a dresser. Because of this, we should expect the first few layers in a neural network to do most of the heavy lifting and learn how to do their job the fastest – because, recall, if a function that does more can easily be learned, it will, and because the functions the first layers learn are applied first. In the language of deep learning: we should expect the lower layers’ parameters to be optimized first. Maithra Raghu observed exactly this phenomenon using (Single Vector Canonical Correlation Analysis). This just shows the predictive power behind thinking about neural networks in this way !
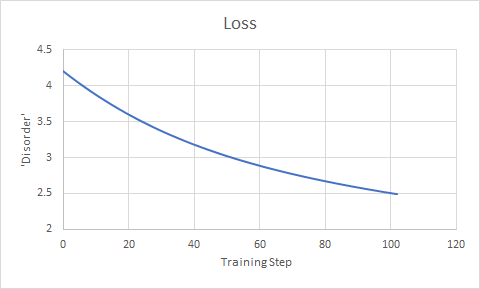
Fig 2. Neural networks are trained by successively reducing the disagreement between its prediction and the real data. This disagreement is called the “Loss.” The loss is measured, then parameters specifying the details of the network at tweaked a little to try to reduce the loss; then, the process is repeated.
The two real takeaways here are: 1) we don’t need to have specific data in mind to talk about the vector structure of layers in a neural network and 2) neural networks certainly aren’t black boxes, and can be designed heuristically by considering how we solve problems, which can, in turn, lead to interesting discoveries. Going forward, I believe we can expect many more predictions to come out of our emerging understanding of neural network.