I recently had the pleasure of attending REWORK’s Deep Learning Summit in Boston. Two topics stood out to me as eminently huge forces in deep learning: a powerful way to understand neural networks (and its practical benefits), and domain adaptation. These are both topics the community should be aware of, so let’s discuss them.
1. Neural Networks Demystified
Neural networks were virtually stumbled upon. They were chiefly motivated by the consistently powerful, yet heuristic, argument that evolution engineered optimized systems, and we should thus emulate those systems when designing our own. While modern implementations of neural nets boast staggering performance, our understanding of their inner workings remains limited – they are somewhat of a “black box”.
However, large strides towards achieving understanding have recently been made. At the conference, Maithra Raghu, a graduate student at Cornell, unveiled research she has been working on with her advisor. She proposes a novel way of interpreting neurons and their linear combinations:
- Each neuron is a vector (very loosely, a collection of numbers whose order matters – like a phone number) whose components (numbers at specific locations in this collection) are just the outputs from the neuron.
- The output of each layer in a neural network is just a sum of the outputs of the neurons in that layer, so this means that we can think of the output of each layer as a vector in what’s called the span of the neurons (the span of some set is simply the collection of all possible ways to sum the members of the set).
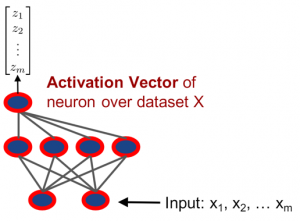
1 The Vector output of a neuron – a graphic from Raghu’s presentation
Leveraging their pedagogical interpretation, Raghu et al debuted a technique they termed SVCCA that analyzes how quickly each layer in a network ‘learned,’ and discovered that the first few layers converge the most quickly. The practicable application: the weights and biases for the earlier layers can be frozen (i.e. not updated) as model training progresses. This reduces the typically massive computational expense of training a neural net, making it more cost effective and scalable!
These results actually shouldn’t be, from a theoretical perspective, surprising. That’s something I’ll explore more in Part 2!
2. Domain Adaptation
I play squash; many of my friends play tennis. I didn’t want to play tennis, so I convinced them to play squash. I figured I would certainly have the upper hand! One of my friends, however, has been my absolute rival in squash since I convinced him to play. This is because, even though squash and tennis are pretty different, it turns out tennis is a remarkably transferable skill since both share hitting a ball with a racket while ensuring the competitor doesn’t. This ability to adapt one learned skill to a different domain seems rather human, right? It turns out machines can do this too; or, at least, they show promise at this juncture using domain adaptation.
Domain adaptation tries to figure out how to adapt a model that’s been trained on one dataset, (the source), so that it works on a similar, but different, dataset, (the target). This typically involves determining the relationship between the source and the target. The basic idea is best explained in terms of what’s called the “manifold hypothesis.”
Other blogs, such as Chris Olah’s, have already masterfully tackled what the manifold hypothesis means in more detail, but the basic premise is: we can think of the values of a data point within a data set as that point’s position in space. The collection of those points lies on what’s called a manifold, which we can in turn think of as the surface of a piece of paper that’s warped and contorted in various ways. The goal of domain adaptation is thus figuring out how to adapt a trained model by relating data on one manifold, the source manifold, to data on another, slightly differently shaped manifold, the target manifold. In particular, domain adaptation attempts to do this for situations in which we have many points on the source manifold and few on the target. That is, when we have a dense data set we’ve trained a model on, and a sparse data set we would like to train a model on (see diagram below).
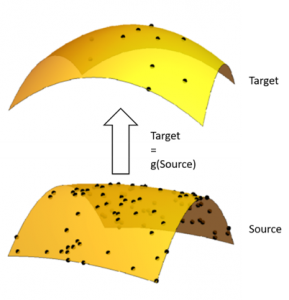
An example of a source data set could be a set of computer generated images of a planet, and the target would be a set of actual pictures of that planet. We likely have few real pictures of the planet, but we could easily generate a lot of images using a model. However, the uncanny valley, typically makes computer generated images close to, but not quite like, their real counter parts. This means that a model trained on the computer generated images might not work on the real ones.
Google Brain flips the problem slightly on its head. They have leveraged a generative adversarial network (GAN), a new type of neural network that excels at creating new things by combining its knowledge of known things, to basically learn a function (pictured above) that takes data points on the source manifold and uses them to augment the data on the target manifold. The value added: it can be used to populate a sparse target dataset so that a model can be trained on it!
This method can be used to aid in training a model if there is a dearth of available data needed for that model. This is a common problem, for example, attempting to analyze and predict on data in the medical and healthcare space, where the number of patients (data points) is limited. This approach to domain adaptation is also the first step towards creating a computer skilled at tennis that can beat me in squash!
Comments, ideas, questions? Contact us at: info@www.excella.com.